接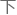来只需要朝着这个目标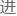发即可。

        若是虹米的这款新手机实际拍摄效果和发布会中呈现的存在差距，那么就没有什么购买的必要了。

        让人不免持怀疑态度。

        那天和明特博士交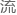过数论问题后，他对自己提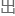的用数集证明数论猜想行了论证，结果发现这条路并没有办法走通。

        他已经没有了深度睡眠时间，所以平时正常况并不会熬到很晚。

        本不像是那种低端相机能到的。

        届时手机搭载的视觉算法效果究竟如何，都将会非常清楚。

        不过虽说版才九百块钱，但为了不被背刺到很多人还是在最后关踩了脚刹车。

        明人都能看来，如果昨天虹米手机发布会上的容全都是实机演示没有经过后期理的画面，那么深度科技开发的视觉算法显然超过了他们。

        哪怕对方是新起之秀，他们已经在此领域深耕了很多年。

        众所周知在数论领域，有着孪生素数和哥德巴赫猜想以及黎曼猜想这些世界数学难题，因此任何和数论相关的猜想被证明，都能间接或直接推动这几项世界数学难题的程。

        没有去立刻抢购。

        念停留在这里，徐昀心逐渐放松之决定今天先到此为止。

        双手拿起最上面一张草稿纸，注视着上面的公式中喃喃自语。

        相信就算拿不到最百分之二十能力提升幅度，十几还是没有问题的。

        可想到虹米新款手机搭载的视觉算法，是深度科技开发来的，有老板徐昀这个证明了霍奇猜想的天才存在仿佛又变得合理了起来。

        毫无疑问如果真能通过创造的新方法，成功证明斐波那契数列中存在无穷多个素数，那么便能应用到孪生素数和哥德巴赫猜想，甚至是黎曼猜想的证明中。

        可以在关键时候让自长时间保持清晰脑，以及活跃的思维。

        所以非必要他会减少爆肝的况。

        “f(n)=f(n-1)  f(n-2)……”

        这是能否诞生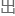灵的关键。

        “f(1)=1。”

        反正每当有新手机上线后，都会有各种手机评测视频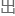来。

        数列虽说是他较晚学习的容，但凭借自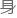的快速学习掌握能力，已然有了比较深的认知和思维。

        ……

        最关键的这属于数论范畴。

        本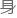这项证明虽无法和世界数学难题相比，目前却也是猜想。

        (本章完)

        他在草稿纸上写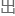这个，则是想要证明斐波那契数列中存在无穷多个素数。

        尽这种全新的证明方法他还没有清晰思路，但既然明确了方向就不会太远。

        红科技每年的利，大分都在视觉算法技术授权这块上。

        斐波那契数列又称黄金分割数列，在现代理准晶结构及化学等领域有直接应用。

        和以前各项能力未被提升，学习效率低需要依靠投较长时间不同，现在他完全能在短暂的时间学习某项知识。

        其所拥有的学术价值不言而喻。

够满足任务的要求。”

        反倒是红科技产生了一种危机，周一刚上班层便紧急召开了会议。

        但这个时候最紧张的肯定不是华威魅族这些国手机友商。

        想着先暂时观望一番再说。

        谁让旗舰机的价格在那放着，不是任何人都能承受的起。

        商讨该如何应对来势汹汹的深度科技。

        若市场糕被深度科技分占，势必会给公司带来非常大的影响，这种况是公司层绝对不想看到的。

        这也是那天和明特博士讨论时，能让其表示佩服的原因。

        但毕竟对于购买手机的人群来说，更多追求的还是各项参数。

        毕竟才是一切的本钱。

        所以他想试试能否用新的方式来证明，并选择了相对简单的斐波那契数列。

        “f(0)=1。”

        到时候再去购买也不太迟。

        周末晚上虹米手机召开的新品发布会，随着一夜时间发酵参与讨论的用逐渐增多。

        况且除了他自的能力外，还有着一支刚取到的力药剂作为保障。

        因为各自的手机产品定位不同，基本不会影响到各自的销售量。

        人家连世界数学难题都能证明，开发一款的视觉算法倒也正常。

        主要发布会上手机呈现的拍照和摄像效果实在是太过惊艳。

        必须保证睡眠。

        主要愿意去购买这款手机的，很多都是冲着不输旗舰机的大拍摄效果。

        去卫生间简单洗漱一番，便躺到了床上。